[혼공머신] 3주차: 로지스틱 회귀 & SGD, 분류 알고리즘

지난주에 숫자 예측(회귀)을 다뤘다면, 이번 주에는 데이터를 정해진 기준에 따라 구분하는 ‘분류(Classification)’알고리즘에 대해 깊이 있게 탐구했습니다.
특히 로지스틱 회귀와 확률적 경사 하강법이라는 핵심 개념들을 배우면서, 머신러닝이 어떻게 디어터를 똑독하게 나누고 판단하는지 그 원리를 이해하게 되어 기뻤습니다.
Chapter 04. 다양한 분류 알고리즘
이번 챕터에서는 데이터를 효율적으로 분류하는 여러 가지 기법들을 배웠습니다. 단순히 결과를 아는 것을 넘어, 각 분류기가 어떻게 작동하는지 코드와 함께 들여다보니 훨신 명확하게 다가왔습니다.
04-1 로지스틱 회귀
처음에는 이름에 ‘회귀’가 들어가서 헷갈렸지만, 로지스틱 회귀는 사실 분류에 사용되는 강력한 알고리즘입니다. 이 친구의 가장큰 매력은 단순히 ‘예/아니오’로 분류하는 것을 넘어, 특정 분류 결과에 대한 ‘확률’까지 제시해준다는 점이었습니다. 교재에서 ‘럭키백의 확률’을 예측하는 과정과 유사합니다.
이 물고기가 ‘농어’라고 예측했다면, 그것이 “농어일 확률이 98%야!”와 같이 말이죠. 덕분에 예측에 대한 신뢰도를 파악하고 더 나은 의사결정을 내릴 수 있다는 점이 인상 깊었습니다. 로지스틱 회귀가 이런 확률을 계산하는 비밀은 시그모이드(Sigmoid) 함수에 있습니다. 이 함수는 모델이 계산한 ㅅ너형 방정식의 결과를 0과 1 사이의 값으로 변환해 확률을 나타냅니다. 또한 두 개 이상의 클래스를 분류하는 다중 분류에서는 소프트맥스(Softmax) 함수가 사용되어 모든 클래스의 확률 합이 1이 되도록 만들어 줍니다.
아래 코드는 로지스틱 회귀의 핵심 기능을 보여줍니다.
from sklearn.linear_model import LogisticRegression
from scipy.special import expit, softmax
# 로지스틱 회귀 이진 분류 (Bream과 Smelt)
# 'Bream'과 'Smelt' 두 종류의 생선만 선택하여 이진 분류 데이터셋 준비
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
lr_binary = LogisticRegression()
lr_binary.fit(train_bream_smelt, target_bream_smelt)
print("--- 이진 분류 예측 결과 ---")
print(lr_binary.predict(train_bream_smelt[:5]))
print(np.round(lr_binary.predict_proba(train_bream_smelt[:5]), decimals=4))
# 결정 함수(decision_function) 및 expit 변환
decisions_binary = lr_binary.decision_function(train_bream_smelt[:5])
print("--- 결정 함수 및 expit 변환 ---")
print(np.round(decisions_binary, decimals=2))
print(np.round(expit(decisions_binary), decimals=4))
# 다중 분류 로지스틱 회귀
lr_multi = LogisticRegression(C=20, max_iter=1000)
lr_multi.fit(train_scaled, train_target)
print("--- 다중 분류 모델 점수 ---")
print(lr_multi.score(train_scaled, train_target))
print(lr_multi.score(test_scaled, test_target))
# 다중 분류 결정 함수 및 softmax 변환
decision_multi = lr_multi.decision_function(test_scaled[:5])
print("--- 다중 분류 결정 함수 및 softmax 변환 ---")
print(np.round(decision_multi, decimals=2))
proba_softmax = softmax(decision_multi, axis=1)
print(np.round(proba_softmax, decimals=3))[시그모이드 함수 시각화]
z = np.arange(-5, 5, 0.1)
phi = 1 / (1 + np.exp(-z))
plt.plot(z, phi)
plt.xlabel('z')
plt.ylabel('phi')
plt.title('Sigmoid Function')
plt.grid(True)
plt.show()04-2 확률적 경사 하강법
‘확률적 경사 하강법(Stochastic Gradient Descent, SGD)’은 마치 거대한 산을 오르듯, 대규모 데이터를 효율적으로 학습시키는 방법을 알려주었습니다. 데이터를 한 번에 모두 처리하는 대신, 조금씩 나누어(미니 배치) 점진적으로 학습하는 방식이 인상 깊었습니다. 이러한 학습 방식은 ‘온라인 학습’ 이라고도 불리며, 새로운 데이터가 계속 추가되는 환경에서도 유연하게 대응할 수 있다는 것을 깨달았습니다.
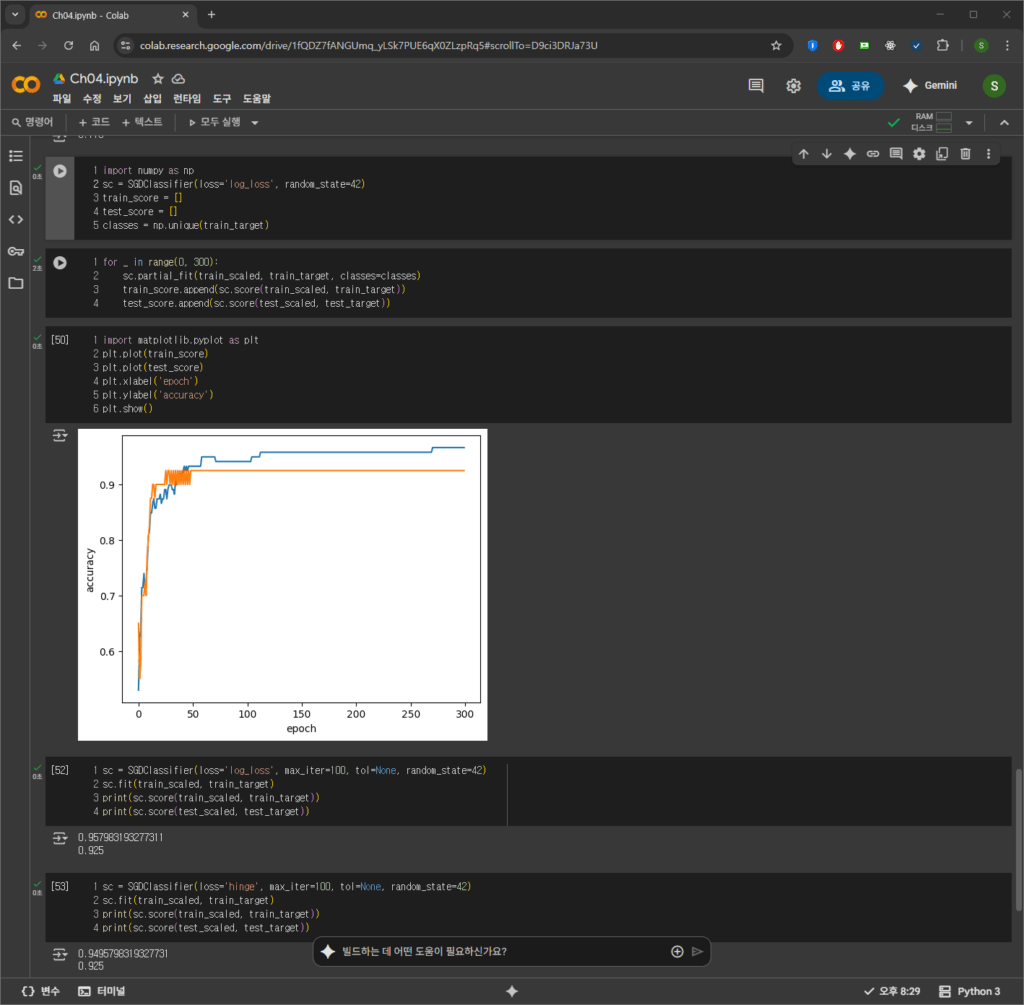
SGDClassifier는 이러한 SGD 방식을 구현한 분류기입니다. partial_fit() 메서드를 사용하면 기존에 학습된 모델에 이어서 추가 학습을 진행할 수 있습니다. 가장 중요하게 느낀 점은 ‘에포크(epoch)’개념과 그것이 모델의 과소적합(underfitting)및 과대적합(overfitting)에 미치는 영향이었습니다. 모델이 전체 훈련 데이터를 몇 번 반복해서 학습했는지 나타내는 에포크 수가 너무 적으면 제대로 학습하지 못하고, 너무 많으면 특정 데이터만 똑똑해져서 오히려 새로운 데이터는 엉뚱한 답을 내놓는다는 사실을 그래프를 통해 시각적으로 확인했습니다. 테스트 세트 점수가 최고점에 도달할 때 학습을 멈추는 조기 종료(Early Stopping) 기법의 중요성도 알게 되었습니다.
아래는 SGDClassifier의 점진적 학습과 에포크에 대한 성능 변화를 보여주는 주요 코드입니다.
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log_loss', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print("--- 초기 SGD 모델 점수 (max_iter=10) ---")
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
sc.partial_fit(train_scaled, train_target)
print("--- partial_fit 후 SGD 모델 점수 ---")
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
sc_curve = SGDClassifier(loss='log_loss', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0, 300):
sc_curve.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc_curve.score(train_scaled, train_target))
test_score.append(sc_curve.score(test_scaled, test_target))
# 최적화된 모델 훈련 (tol=None으로 max_iter만큼 무조건 반복)
sc_final = SGDClassifier(loss='log_loss', max_iter=100, tol=None, random_state=42)
sc_final.fit(train_scaled, train_target)
print("--- 최적화된 SGD 모델 점수 (max_iter=100) ---")
print(sc_final.score(train_scaled, train_target))
print(sc_final.score(test_scaled, test_target))[SGDClassifer 학습 곡선 시각화]
plt.plot(train_score, label='Train Accuracy')
plt.plot(test_score, label='Test Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title('SGDClassifier Learning Curve')
plt.legend()
plt.grid(True)
plt.show()3주차를 마치며
이번 3주차 학습은 저에게 ‘분류’ 알고리즘의 본질을 깊이 이해하는 계기가 되었습니다. 로지스틱 회귀가 ‘확률’을 통해 예측의 섬세함을 더해주고, 확률적 경사 하강법이 ‘점진적 학습’으로 대규모 데이터 처리의 효율성을 높여준다는 점이 정말 매력적이었습니다.
단순히 라이브러리의 함수를 호출하는 것을 넘어, 코드를 통해 각 알고리즘이 어떤 원리로 데이터를 분류한고, 어떤 상황에 왜 사용되는지에 대한 통찰을 얻게 된 것이 가장 큰 수확이라고 생각합니다. 머신러닝 모델의 복잡한 내부 작동 방식을 더욱 명확하게 파악할 수 있게 되어 뿌듯합니다.
기본 숙제(필수): Ch.04(04-1) 확인문제(p.208) 2번 문제 풀고, 설명하기
2. 로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수는 무엇인가요?
① 시그모이드 함수
② 소프트맥스 함수
③ 로그 함수
④ 지수 함수
정답 : 1. 시그모이드 함수 (교재 203p. 로지스틱 회귀는 선형 방정식의 예측값을 시그모이드 함수에 통과시켜 0~1 사이의 확률값(양성 클래스 확률)으로 변환하며, 이것이 정답이 시그모이드 함수인 이유입니다.
추가 숙제(선택): Ch.04(04-2) 과대적합/과소적합 손코딩(p.220) 하고 코랩 화면 캡처하기