[혼공머신] 2주차: 회귀 알고리즘과 모델 규제 실습 후기

‘혼자 공부하는 머신러닝 + 딥러닝 개정판’ 스터디 2주차 학습을 마쳤습니다.
이번 2주차는 교재의 Chapter 03 ‘회귀 알고리즘과 모델 규제’를 중심으로, 숫자를 예측하는 ‘회귀’에 대해 깊이 있게 학습하였습니다. 모델이 과도하게 훈련 데이터에 적합하거나(과대적합) 너무 단순하여 성능이 저하되는(과소적합) 현상을 방지하는 ‘규제’ 기법까지 배우며 머신러닝 모델을 더욱 견고하게 구축하는 방법을 익혔습니다.
Chapter 03. 회귀 알고리즘과 모델 규제
이번 챕터에서는 데이터를 통해 연속적인 숫자를 예측하는 ‘회귀’의 기본 개념부터, 모델의 성능을 향상시키고 일반화하는 다양한 기법들을 실습하였습니다.
03-1 k-최근접 이웃 회귀
첫 시작은 ‘k-최근접 이웃 회귀’였습니다. 주변의 가장 가까운 K개 샘플들의 평균값을 이용하여 새로운 샘플의 값을 예측하는 방식입니다. 농어 무게 예측을 예시로 학습하였는데, 훈련 데이터에 있는 가장 큰 농어의 무게를 벗어나지 못하는 한계가 있었습니다.
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_absolute_error
perch_length = np.array([8.4, 13.7, 15.0, ..., 44.0])
perch_weight = np.array([5.9, 32.0, 40.0, ..., 1000.0])
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)
knr = KNeighborsRegressor()
knr.fit(train_input, train_target)
test_prediction = knr.predict(test_input)
mae = mean_absolute_error(test_target, test_prediction)
print(mae)
print(knr.score(train_input, train_target))
print(knr.score(test_input, test_target))
knr.n_neightbors = 3
knr.fit(train_input, train_target)
print(knr.score(train_input, train_target))
print(knr.score(test_input, test_target))위 코드의 출력 결과를 통해 k-최근접 이웃 회귀는 훈련 세트의 범위를 벗어나는 샘플에 대해서는 새로운 값을 예측하지 못하고, 가장 가까운 이웃들의 평균값을 그대로 사용한다는 한계가 명확하게 드러났습니다.
03-2 선형 회귀
k-최근접 이웃 회귀의 한계를 극복하기 위해 선형 회귀를 학습하였습니다. 데이터의 경향을 가장 잘 나타내는 ‘직선’을 찾아 예측하는 알고리즘입니다. 농어 길이와 무게처럼 특성과 타깃이 선형적인 관계를 가질 때 매우 유용합니다.
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
perch_length = np.array([8.4, ..., 44.0])
perch_weight = np.array([5.9, ..., 1000.0])
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)
knr = KNeighborsRegressor(n_neighbors=3)
knr.fit(train_input, train_target)
print(knr.predict())
print(knr.predict())
lr = LinearRegression()
lr.fit(train_input, train_target)
print(lr.predict())
print(lr.coef_, lr.intercept_)
print(lr.score(train_input, train_target))
print(lr.score(test_input, test_target))
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))
print(train_poly.shape, test_poly.shape)
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]]))
print(lr.coef_, lr.intercept_)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))선형 회귀 모델은 50cm 농어의 무게를 약 1241.8g으로 예측하며, k-최근접 이웃 회귀보다 훨씬 합리적인 예측을 보여주었습니다. 하지만 농어 데이터는 선형 관계보다는 비선형 관계에 가까운 특성을 보였습니다.
그래서 다항 회귀를 사용하였습니다. 특성을 제곱하거나 여러 특성을 곱하여 새로운 특성을 생성하는 ‘특성 공학’을 통해 비선형 관계도 선형 모델로 표현할 수 있습니다. 길이를 제곱한 특성을 추가한 다항 회귀 모델은 50cm 농어의 무게를 약 1574g으로 예측하며, 이러한 다항 특성 추가를 통해 모델이 데이터를 훨씬 더 잘 표현할 수 있었습니다. R² 점수도 크게 향상되어 모델이 데이터를 더 잘 학습하였음을 보여주었습니다.
이처럼 k-최근접 이웃 회귀의 한계를 선형 회귀로, 그리고 선형 회귀의 한계를 다항 회귀로 극복하는 과정을 통해 모델의 성능을 점진적으로 개선하는 방법을 배울 수 있었습니다. 데이터의 특성에 맞는 적절한 알고리즘과 특성 공학의 중요성을 다시 한번 깨달았습니다.
03-3 특성 공학과 규제
이번 챕터의 핵심은 ‘특성 공학’과 ‘규제’였습니다. 실제 농어 데이터에는 길이, 높이, 두께 이렇게 세 가지 특성이 있었는데, 이러한 다중 특성을 활용하는 방법을 학습하였습니다.
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.linear_model import LinearRegression, Ridge, Lasso
import numpy as np
perch_full = pd.read_csv('https://bit.ly/perch_csv_data')
perch_weight = np.array([5.9, 32.0, ..., 1000.0])
train_input, test_input, train_target, test_target = train_test_split(perch_full, perch_weight, random_state=42)
poly_example = PolynomialFeatures()
print(poly_example.transform([[2, 3]]))
poly_example_no_bias = PolynomialFeatures(include_bias=False)
print(poly_example_no_bias.transform([[2, 3]]))
poly = PolynomialFeatures(include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape)
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape)
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)
# 릿지 회귀
ridge = Ridge(alpha=0.1)
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))
# 라쏘 회귀
lasso = Lasso(alpha=10, max_iter=10000)
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))
print(np.sum(lasso.coef_ == 0))PolynomialFeatures 변환기를 사용하여 기존 특성들을 조합하여 새로운 특성을 생성하였습니다. degree=5로 설정하여 5차 다항 특성을 만들었더니 무려 55개의 특성이 생성되었습니다. 이처럼 특성이 많아지면 모델이 훈련 데이터에 너무 과도하게 적합되는 과대적합이 발생할 수 있습니다. 훈련 세트 점수는 거의 완벽하지만, 테스트 세트 점수는 하락하여 과대적합이 명확하게 나타났습니다.
규제 (Regularization)
이러한 과대적합을 해결하기 위해 ‘규제’를 적용합니다. 규제는 모델이 훈련 세트에 너무 과하게 적합되지 않도록 가중치(계수)를 제한하는 방법입니다. 규제를 적용하기 전에 StandardScaler로 특성들의 스케일을 맞춰주는 표준화 과정을 거쳤습니다.
릿지 회귀 (Ridge Regression)
릿지 회귀는 계수의 제곱합을 규제에 사용합니다. 계수들을 0에 가깝게 만들지만 완전히 0으로 만들지는 않습니다. 릿지 회귀를 통해 테스트 세트 점수가 크게 향상되어 과대적합이 줄어들었음을 알 수 있었습니다.
라쏘 회귀 (Lasso Regression)
라쏘 회귀는 계수의 절댓값 합을 규제에 사용합니다. 릿지와 달리, 중요하지 않은 특성의 계수를 아예 0으로 만들어 특성 선택 효과까지 얻을 수 있습니다. 라쏘 모델 또한 좋은 성능을 보여주며 과대적합을 줄였으며, 실제로 많은 특성의 계수를 0으로 만들어 불필요한 특성을 제거하는 효과를 확인하였습니다.
2주차를 마치며
‘혼자 공부하는 머신러닝 + 딥러닝 개정판’ 2주차 학습을 통해 회귀 알고리즘의 기본 원리부터 모델의 성능을 개선하고 과대적합을 제어하는 ‘규제’ 기법까지, 정말 폭넓은 지식을 습득하였습니다. 특히 데이터를 변환하고 새로운 특성을 만들어내는 ‘특성 공학’은 머신러닝 모델링에서 얼마나 중요한지 다시 한번 깨닫게 되었습니다. 이론 학습과 실습 코드를 병행하며 머신러닝 모델을 더 견고하게 만드는 핵심 원리를 효과적으로 이해할 수 있었습니다. 이제 모델이 왜 잘 작동하는지, 왜 가끔 이상한 결과를 내는지 조금은 알 것 같은 느낌입니다.
기본 숙제(필수): Ch.03(03-1) 확인문제(p.135) 4번 출력 그래프 인증하기
knr = KNeighborsRegressor()
x = np.arange(5, 45).reshape(-1, 1)
for n in [1, 5, 10]:
knr.n_neighbors = n
knr.fit(train_input, train_target)
prediction = knr.predict(x)
plt.scatter(train_input, train_target)
plt.plot(x, prediction)
plt.title('n_neighbors = {}'.format(n))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()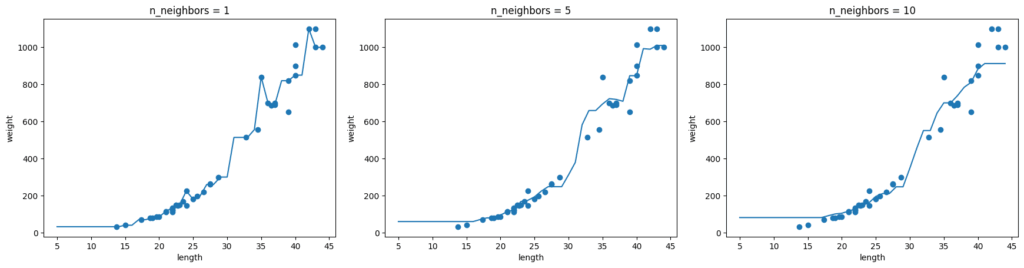
추가 숙제(선택): 모델 파라미터에 대해 설명하기
모델 파라미터는 머신러닝 모델이 훈련 데이터를 학습하며, 각 특성이 결과에 미치는 영향을 수치화하여 스스로 찾아낸 값들입니다. 이는 선형 회귀의 가중치처럼 모델이 데이터를 통해 얻는 핵심적인 ‘지식’이며, 훈련 과정에서 자동으로 최적화됩니다.

